The intuition for the exponential number e
Exponential functions have the form bx, where b > 0 is the base and x the exponent.
Exponential functions are easily introduced as growth processes. The comparison of x² and 2^x is an eye-opener, with the stories of duckweed or the grain on the chess board. The introduction of the exponential number e is a next step. What intuitions can we use for smooth didactics on e ?
The “discover-e” plot
There is the following “intuitive graph” for the exponential number e = 2,71828…. The line y = e is found by requiring that the inclines (tangents) to y = bx all run through the origin at {0, 0}. The (dashed) value at x = 1 helps to identify the function ex itself. (Check that the red curve indicates 2^x).
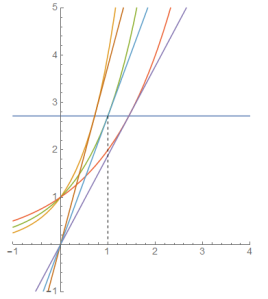
2^x, e^x and 4^x, and inclines through {0, 0}
Remarkably, Michael Range (2016:xxix) also looks at such an outcome e = 2^(1 / c), where c is the derivative of y = 2^x at x = 0, or c = ln[2]. NB. Instead of the opaque term “logarithm” let us use “recovered exponent”, denoted as rex[y].
Perhaps above plot captures a good intuition of the exponential number ? I am not convinced yet but find that it deserves a fair chance.
NB. Dutch mathematics didactician Hessel Pot, in an email to me of April 7 2013, suggested above plot. There appears to be a Wolfram Demonstrations Project item on this too. Their reference is to Helen Skala, “A discover-e,” The College Mathematics Journal, 28(2), 1997 pp. 128–129 (Jstor), and it has been included in the “Calculus Collection” (2010).
Deductions
The point-slope version of the incline (tangent) of function f[x] at x = a is:
y – f[a] = s (x – a)
The function b^x has derivative rex[b] b^x. Thus at arbitrary a:
y – b^a = rex[b] b^a (x – a)
This line runs through the origin {x, y} = {0, 0} iff
0 – b^a = rex[b] b^a (0 – a)
1 = rex[b] a
Thus with H = -1, a = rex[b]H = 1 / rex[b]. Then also:
y = f[a] = b^a = b^rex[b]H = e^(rex[b] rex[b]H) = e^1 = e
The inclines running through {0, 0} also run through {rex[b]H, e}. Alternatively put, inclines can thus run through the origin and then cut y = e .
For example, in above plot, with 2^x as the red curve, rex[2] ≈ 0.70 and a ≈ 1.44, and there we find the intersection with the line y = e.
Subsequently also at a = 1, the point of tangency is {1, e}, and we find with b = e that rex[e] = 1,
The drawback of this exposition is that it presupposes some algebra on e and the recovered exponents. Without this deduction, it is not guaranteed that above plot is correct. It might be a delusion. Yet since the plot is correct, we may present it to students, and it generates a sense of wonder what this special number e is. Thus it still is possible to make the plot and then begin to develop the required math.
Another drawback of this plot is that it compares different exponential functions and doesn’t focus on the key property of e^x, namely that it is its own derivative. A comparison of different exponential functions is useful, yet for what purpose exactly ?
Descartes
Our recent weblog text discussed how Cartesius used Euclid’s criterion of tangency of circle and line to determine inclines to curves. The following plots use this idea for e^x at point x = a, for a = 0 and a = 1.
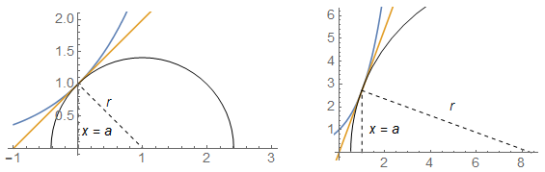
Incline to e^x at x = 0 (left) and x = 1 (right)
Let us now define the number e such that the derivative of e^x is given by e^x itself. At point x = a we have s = e^a. Using the point-slope equation for the incline:
y – f[a] = s (x – a)
y – e^a = e^a (x – a)
y = e^a (x – (a – 1))
Thus the inclines cut the horizontal axis at {x, y} = {a – 1, 0}, and the slope indeed is given by the tangent s = (f[a] – 0) / (a – (a – 1)) = f[a] / 1 = e^a.
The center {u, 0} and radius r of the circle can be found from the formulas of the mentioned weblog entry (or Pythagoras), and check e.g. a = 0:
u = a + s f[a] = a + (e^a)²
r = f[a] √ (1 + s²) = e^a √ (1 + (e^a)²)
A key problem with this approach is that the notion of “derivative” is not defined yet. We might plug in any number, say e^2 = 10 and e^3 = 11. For any location the Pythagorean Theorem allows us to create a circle. The notion of a circle is not essential here (yet). But it is nice to see how Cartesius might have done it, if he had had e = 2.71828….
Conquest of the Plane (COTP) (2011)
Conquest of the Plane (2011:167+), pdf online, has the following approach:
- §12.1.1 has the intuition of the “fixed point” that the derivative of e^x is given by e^x itself. For didactics it is important to have this property firmly established in the minds of the students, since they tend to forget this. This might be achieved perhaps in other ways too, but COTP has opted for the notion of a fixed point. The discussion is “hand waiving” and not intended as a real development of fixed points or theory of function spaces.
- §12.1.2 defines e with some key properties. It holds by definition that the derivative of e^x is given by e^x itself, but there are also some direct implications, like the slope of 1 at x = 0. Observe that COTP handles integral and derivative consistently as interdependent notions. (Shen & Lin (2014) use this approach too.)
- §12.1.3 gives the existence proof. With the mentioned properties, such a number and function appears to exist. This compares e^x with other exponential functions b^x and the recovered exponents rex[y] – i.e. logarithm ln[y].
- §12.1.4 uses the chain rule to find the derivatives of b^x in general. The plot suggested by Hessel Pot above would be a welcome addition to confirm this deduction and extension of the existence proof.
- §12.1.5-7 have some relevant aspects that need not concern us here.
- §12.1.8.1 shows that the definition is consistent with the earlier formal definition of a derivative. Application of that definition doesn’t generate an inconsistency. No limits are required.
- §12.1.8.2 gives the numerical development of e = 2.71828… There is a clear distinction between deduction that such a number exists and the calculation of its value. (The approach with limits might confuse these aspects.)
- §12.1.8.3 shows that also the notion of the dynamic quotient (COTP p57) is consistent with above approach to e. Thus, the above hasn’t used the dynamic quotient. Using it, we can derive that 1 = {(e^h – 1) // h, set h = 0}. Thus the latter expression cannot be simplified further but we don’t need to do so since we can determine that its value is 1. If we would wish so, we could use this (deduced) property to define e as well (“the formal approach”).
The key difference between COTP and above “approach of Cartesius” is that COTP shows how the (common) numerical development of e can be found. This method relies on the formula of the derivative, which Cartesius didn’t have (or didn’t want to adopt from Fermat).
Difference of COTP and a textbook introduction of e
In my email of March 27 2013 to Hessel Pot I explained how COTP differed from a particular Dutch textbook on the introduction of e.
- The textbook suggests that f ‘[0] = 1 would be an intuitive criterion. This is only partly true.
- It proceeds in reworking f ‘[0] = 1 into a more general formula. (I didn’t mention unstated assumptions in 2013.)
- It eventually boils down to indeed positing that e^x has itself as its derivative, but this definition thus is not explicitly presented as a definition. The clarity of positing this is obscured by the path leading there. Thus, I feel that the approach in COTP is a small but actually key innovation to explicitly define e^x as being equal to its derivative.
- It presents e only with three decimals.
Conclusion
There are more ways to address the intuition for the exponential number, like the growth process or the surface area under 1 / x. Yet the above approaches are more fitting for the algebraic approach. Of these, COTP has a development that is strong and appealing. The plots by Cartesius and Pot are useful and supportive but no alternatives.
The Appendix contains a deduction that was done in the course of writing this weblog entry. It seems useful to include it, but it is not key to above argument.
Appendix. Using the general formula on factor x – a
The earlier weblog entry on Cartesius and Fermat used a circle and generated a “general formula” on a factor x – a. This is not really factoring, since the factor only holds when the curve lies on a circle.
Using the two relations:
f[x] – f[a] = (x – a) (2u – x – a) / (f[x] + f[a]) … (* general)
u = a + s f[a] … (for a tangent to a circle)
we can restate the earlier theorem that s defined in this manner generates the slope that is tangent to a circle.
f[x] – f[a] = (x – a) (2 s f[a] – (x – a)) / (f[x] + f[a])
It will be useful to switch to x – a = h:
f[a + h] – f[a] = h (2 s f[a] – h) / (f[a + h] + f[a])
Thus with the definition of the derivative via the dynamic quotient we have:
df / dx = {Δf // Δx, set Δx = 0}
= {(f[a + h] – f[a]) // h, set h = 0}
= { (2 s f[a] – h) / (f[a + h] + f[a]), set h = 0}
= s
This merely shows that the dynamic quotient restates the earlier theorem on the tangency of a line and circle for a curve.
This holds for any function and thus also for the exponential function. Now we have s = e^a by definition. For e^x this gives:
ea + h – ea = h (2 s ea – h) / (ea + h + ea)
For COTP §12.1.8.3 we get, with Δx = h:
df / dx = {Δf // Δx, set Δx = 0}
= {(ea + h – ea ) // h, set h = 0}
= {(2 s ea – h) / (ea + h + ea) , set h = 0}
= s
This replaces Δf // Δx by the expression from the general formula, while the general formula was found by assuming a tangent circle, with s as the slope of the incline. There is the tricky aspect that we might choose any value of s as long as it satisfies u = a + s f[a]. However, we can refer to the earlier discussion in §12.1.8.2 on the actual calculation.
The basic conclusion is that this “general formula” enhances the consistency of §12.1.8.3. The deduction however is not needed, since we have §12.1.8.1, but it is useful to see that this new elaboration doesn’t generate an inconsistency. In a way this new elaboration is distractive, since the conclusion that 1 = {(e^h – 1) // h, set h = 0} is much stronger.
