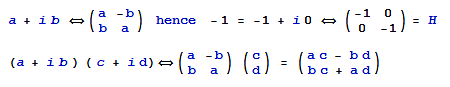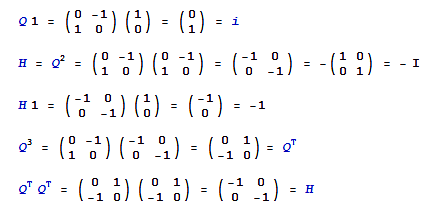Edward Frenkel’s “love” reaches Holland

Chronologically:

• In October 2014 I explained that Edward Frenkel abused “love” with his book “Math & Love“. As a mathematician he has no training in the empirical science of mathematics education, and what he states about mathematics education is often delusional. The situation is rather typical of the arrogance that is so common among mathematicians. The attitude is “the best way to teach and learn mathematics is to do mathematics”, but this confuses the context of mathematics research with the context of education. See here for a recent comment on the USA Common Core for mathematics.
• In November 2015, Dutch NRC Handelsblad science journalist Margriet van der Heijden discussed the book, labeled him a “glamour-nerd” and expressed doubts about his book as a “cocktail of superficial superlatives, incomprehensible math and touching memories of his youth”. Unfortunately, Van der Heijden did not explicitly mention the gap between mathematics research and education in mathematics.
• In April 2016, Dutch NRC Handelsblad USA correspondent Diederik van Hoogstraten recycled the story, flew from Los Angeles to San Francisco and drank wine with Frenkel, resulting in this interview. The catchy title of the interview is “Math anxiety ? Don’t be afraid anymore !” Apparently professor Frenkel has found the medicine that we have all been waiting for. The label “rockstar-mathematician” is used (in quotes), and while there is proper reference to the criticism by Margriet van der Heijden, Frenkel gets the last word to state the good intentions of his book.

“It has to go wrong only once. You must solve a problem in arithmetic in front of the class. You can’t do it. You are scolded, because we are focused on the result and the result was wrong. You feel dumb. A nightmare. (…) Then you are afraid for the rest of your life. Afraid to make an error and be “dumb”. This is a shame, for it is a wonderful subject. In this way we deny millions of people this knowledge, wisdom and beauty. (…) I want to find a way to the heart of all those people with youth trauma’s. It is okay, I say, you don’t have to be afraid.” (Edward Frenkel, NRC 2016-04-23, my translation)

It may well be that there are still many math teachers who abuse their students, but we must wonder whether Frenkel bases his view upon statistics or folklore. Normal teachers tend to ask up front only those students who are likely to get the result (e.g. have shown this already on paper). The normal discussion is on method and not merely on result. Thus Frenkel’s view on “math anxiety” is rather folklore than a result of research in current mathematics education. Subsequently, people with math anxiety will not read and be cured by a book that has so much mathematics, however much “love” you will put in the title. Both diagnosis and treatment are delusional.

Dutch is a language sink. Why was it considered useful to translate this delusional book from English into Dutch ? Would there really be readers who would grasp Frenkel’s math but not be able to read English ? Translators from English into Dutch have an easy job, and publishers can piggy-back upon international bestsellers. It is more difficult to translate from Dutch into English, and market this in the English reading world, but it would be more relevant to open up Holland to the world. Why did Van Hoogstraten want to interview Frenkel ? Perhaps the Dutch publisher of the Dutch translation sent him a copy of the book with Frenkel’s telephone number ? Alongside money laundering there is also delusional book laundering (that sells for cash too).

This is not without cost.

• NRC Handelsblad has misinformed its readership twice now. Readers who have the idea that mathematics is inaccessible actually have seen this idea confirmed.
• There is nothing in their reports on Frenkel that explicitly shows that mathematics is accessible to more people than commonly thought, albeit that this can be found elsewhere and not with Frenkel.
• NRC Handelsblad has never reported on my books since 2009 on mathematics education. The newspaper likely finds mathematics sexy and mathematics education both boring and no science.

Holland is not an open minded country. Holland is a country where books are sold that have been translated into Dutch.

Edward Frenkel in 2010 (wikimedia commons)

Teaching square root and complex number (re-engineered)

My book Elegance with Substance (EWS) (2009, 2015) (pdf online) has the theme that mathematics education requires fundamental re-engineering. Mathematicians are trained to think abstractly and are not trained for the empirical science of didactics. When they meet real life students in class, mathematicians suffer from cognitive dissonance, and resolve this by sticking to traditional ways of teaching, which tradition has not been designed for optimal didactics. In this manner, mathematics education is in shambles for some 5000 years.

One of the reasons why complex numbers are considered difficult – or difficult to teach – is that the traditional presentation of the square root is crummy. For this, see EWS p26 & p30.

• An author may presume that readers of some chapter in a book (EWS) have read the preceding chapters. In a weblog, such an assumption is rather risky.
• Please read EWS, for this already contains subtle discussion. When you have read EWS you better understand my intentions and what steps have been taken already. This will allow me to build upon what has been said before.
• In this weblog I am forced to repeat issues nevertheless, for I cannot assume that you have read EWS or earlier weblog entries.
• Let us make the best of this. For now, at least check out the earlier discussion of the quadratic function.

Metaphor

Math teacher John goes to school by vehicle, either car or bike. Since he uses his car more often he calls it “the” vehicle, and his bike “the other” vehicle. His class knows that he does so. One day, John goes to school by bike and hits a rock that bends the front wheel. Arriving late in class he explains: “Today I came by bike and had an accident. The vehicle was severely damaged and I had to walk.” Most students accept this explanation but some are inclined to mathematics or litigation, and they ask: “How can it be that you came by bike and that your car was severely damaged ?”

The idea that the word “the” could be reserved only for one vehicle conflicts with reality. The term “the” is used much more flexible in human discourse than one can really fix differently.

Correct in wikipedia

Wikipedia is not quite an encyclopedia but rather a portal to proper sources. In this case however it provides a proper definition of square root. I only edit the text to get the common {x, y} notation.

“(…) a square root of a number y is a number x such that x² = y, in other words, a number x whose square (…) is y. (…) For example, 4 and −4 are square roots of 16 because 4² = (−4)² = 16.” (wikipedia, edited)

Note two aspects:

• This is solving an equation. In Wolfram Alpha Solve[y = x^2, x].
  
• This can be done algebraically. If you want a numerical result, use N[Solve[y = x^2, x]]

Confusing in wikipedia

Subsequently, wikipedia correctly restates what mathematicians are doing. Both generate confusion.

• “Every non-negative real number y has a unique non-negative square root, called the principal square root, which is denoted by √y, where √ is called the radical sign or radix. For example, the principal square root of 9 is 3, denoted √9 = 3, because 3² = 3 × 3 = 9 and 3 is non-negative.”
  
• “Every positive number y has two square roots: √y, which is positive, and −√y, which is negative. Together, these two roots are denoted ± √y (see ± shorthand). Although the principal square root of a positive number is only one of its two square roots, the designation “the square root” is often used to refer to the principal square root.” (wikipedia, edited)

When teachers wonder why students have problems with square roots then teachers should look at themselves. It are they themselves who have introduced ambiguity by distinguishing the square root versus any square root. This distinction is okay for students who like litigation or mathematics, but it is too subtle for students who are still struggling to understand what the discussion is about.

Note two aspects:

• √y is a function from the set of nonnegative real numbers to itself.
• This can be in algebra while a numerical result is N[√y]. For example √2 ≈ 1.414…

Function or correspondence

Students in highschool learn only about functions. For each input in a function there is only one outcome. There are also correspondences such that an input can have more outcomes. Solving an equation x² = y can have more outcomes and thus it is a correspondence. Since textbooks do not want to discuss correspondences, the distinction is hushed up.

It is better to be explicit about it. Thus, let the correspondence be defined as follows:

Do√y = ± √y   since  (± √y)² = y .   This merely rewrites Solve[y = x², x].

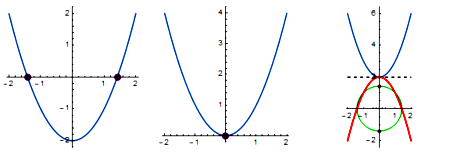
The inverse of function f is function g such that subsequent application returns the original input, thus g[f[x]] = x. The inverse can be found by mirroring alongside the line y = x. The distinction between function and correspondence also explains why the inverse of y = x² gives the correspondence y = Do√x = ± √x (check the switch in the labels of y and x). 

y = x^2 and inverse correspondence y = DoSqrt[x]

Verb and noun

EWS links above notions to the linguistic distinction between verb and noun.

• The correspondence Do√y is like a verb and the function √y is like a noun.
• The algebraic solution √2 is a noun and using the square root sign as an instruction for the calculator is like a verb (outcome 1.414…).
• See Gray & Tall on the notion of the “procept” (process & concept) (verb and noun). The idea of the procept is that mathematics deliberately uses few symbols but with different meanings depending upon context. Teachers tend to treat those contexts implicitly, leaving students to guess what is happening. It is better to introduce more symbols that are explicit about the meaning, like the distinction between function √ and correspondence Do√.

Solution of the abuse of “the”

We diagnose that mathematicians introduce confusion themselves. In highschool they explain what a function is and what solving an equation is, but they do not dwell on the difference between function versus correspondence (and employ such for solving an equation). They encode the hidden intention by introducing an artificial distinction between “the” and “any” root. The latter doesn’t work because language doesn’t not co-operate. For some 3000 years students have been suffering because math teachers have been behaving like Humpty Dumpty in Alice in Wonderland, Through the Looking-Glass, holding that language must adapt to their needs rather than the reverse. Source: wikipedia:

 “When I use a word,” Humpty Dumpty said, in rather a scornful tone, “it means just what I choose it to mean—neither more nor less.”
    “The question is,” said Alice, “whether you can make words mean so many different things.”
    “The question is,” said Humpty Dumpty, “which is to be master—that’s all.”

The obvious solution is to ditch this artificial distinction between “the” and “any” root.

Instead of saying that √4 = 2 is “the root of 4“, it is better to say that it is “the root function value of 4“. Since square roots may also be taught in elementary school, another expression is “rootsign 4“.

Subsequent drama of complex numbers

Complex numbers are not difficult, hardly different from the system of co-ordinates itself, and they are actually quite enlightening since they allow working in the plane directly. Teaching the square root for real numbers however is bodged up in traditional didactics, and hence there is the subsequent drama for complex numbers. The square root of -1 becomes incomprehensible, and the train runs into a mountain.

Merely giving the following definitions is begging for problems.

• Let H = -1, see here. The negative numbers can be created by turning the positive numbers a half turn.
  
• Let H have two roots: i^2 = H and  (-i)^2 = H.
• Let √ now be a function from all real numbers y to the complex numbers z = x + y’ i.
• Let i = √H.

Our earlier discussion of the complex numbers mentioned the danger. Consider:

-1 = H = i²  = (√H) (√H) = √(H H) = √1 = 1 = –H            (*)

Obviously, -1 = 1 doesn’t work for real numbers. Common discussions of this deduction are fraught with problems. They explain that it doesn’t work but not why, or give a curious reason why.

Developing better didactics

When students better understand square roots, then above definitions are easier to extend upon.

The reference to William Rowan Hamilton (1805-1865) and the unit circle is standard, but I have not yet seen the following explanation for above conundrum (*). Rowan Hamilton provided a proper development for complex numbers, namely with the model that z = {x, y} and i = {0, 1}. The crux lies in a particular interpretation of multiplication which neatly fits the theory of angles (trigonometry). A multiplication by i can be interpreted as a quarter turn.

Multiplication of points {a, b} = a + b i and {c, d} = c + d i, gives:

{a, b} {c, d} = (a + b i) (c + d i) = a c + b d i^2 + (a d + b c) i

• Choosing a = d = 1 and b = c = 0 gives {1, 0} {0, 1} = i, which is a quarter turn.
• Choosing a = c = 0 and b = d = 1 gives {0, 1} {0, 1} = i^2, which are two quarter turns = half turn. Thus i^2 = -1.

Hence the general formula becomes:

{a, b} {c, d} = (a + b i) (c + d i) = a c – b d + (a d + b c) i = {a c – b d, a d + b c}

• Starting from {1, 0} and turning counterclockwise along the unit circle in steps of i, we find the outcomes of i, H, -i, and return to 1.
• Clockwise in steps of –i, we find the outcomes of –i, (-i)² = H, (–i)³ = i and back to 1.

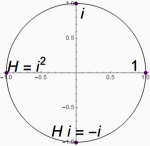The conundrum (*) can now be explained:

• In terms of reals, H = –H only works when H = 0.
• When H means a half turn counterclockwise then –H means a half turn clockwise, and both generate the same result. Thus H = -H makes sense in terms of turning. (Creating the negative numbers from positive numbers x by using –x = H x can be done, but we may also allow for -x = –H x. To make this consistent, we require a more developed theory on rotations.)

Now that we understand why the H = –H outcome arises, we still find the situation paradoxical (without such a theory of rotations), and we decide to obliterate this outcome, so that we do not have to worry about it. This can be done with these definitions:

• When y < 0 then √y = i √ |y|  where |y| gives the absolute value.
• When y < 0 and w < 0 then y w > 0 and √(y w) ≠ √y √w.   PM. The latter is i√|y|  i√|w| = – √ |y w|
• When y < 0 then Do√y = ± i √ |y|

Now deduction (*) is blocked: the step in the middle violates the rule for y < 0 and w < 0. The blockage is no mystery: we decided to choose it in this manner.

The rule for y < 0 and w < 0 causes the main conceptual issue for complex numbers. For example, what to do with √(-2) √(-3) ? Does it solve into √6 ? No, we have chosen to block this solution. The general rule now is to first substitute for i before doing something else. Then √(-2) √(-3) solves as i√2 i√3 = -√6. (There are various expositions online that show the proper calculation steps, e.g. this video. But showing how it is done is not explaining why it is done so.)

With this explanation of (1) what H = –H means and (2) that we block it deliberately,  I wonder whether Rowan Hamilton only gave a different model, so that there is no true difference between x + i y and {x, y}. The models may be fully equivalent, and choosing i = {0, 1} only turns equivalence into identity.

Some PM points

PM 1. This discussion extends on the discussion of complex numbers in EWS p43. (That page uses {1, 2} + {3, 4} = {4, 6}, and the subsequent discussion has an awkward typing error.) A proof of concept is in Conquest of the Plane, p115.

PM 2. Observe that wikipedia has a long lemma on complex numbers and that the rule on y w only appears in notes to another lemma on square roots. Wikipedia is a portal and no textbook, but the rule still is an elementary part of the definition of i = √H. Perhaps the rule seems less relevant when you start from i = {0, 1} but you are bound to need it.

PM 3. A discussion here confuses √y with Do√y, and it argues that we have only:

• Do√H  Do√H = (± i) (± i) = ± (-1) = ±1
• Do√(H H) = Do√1 = ±1.

There is this equality for Do√ indeed, but this doesn’t explain why it fails for √. The subsequent discussion at that website is a bit clearer: “Of course, you can choose to define the square root of a negative number to be a positive multiple of i; but if your book hasn’t done that, it doesn’t have a right to ask this question.” It is okay to establish the freedom for such a definition. The crux however is why one would make it. That website leaves this open. (Our own explanation above is that it avoids confusion on H = –H, which is true for rotations but not for real values.)

PM 4. A reader alerted me to it that the common discussion of the complex solution to the quadratic function uses a projection from the Argand plane onto the Cartesian plane. I was aware of this, but let me pass on the links, provided in this alert, to these two papers by Ansie Harding and Johann Engelbrecht: one and two.

PM 5. Dutch readers can benefit from a discussion by J.H. Wansink, “De complexe getallen. Een algebraisch onderwerp op dood spoor“,  Euclides 51e jaargang no 4, 1975/1976, p127-149. Wansink is very positive about the way of presenting complex numbers as analytic geometry as had been done by H.J.E. Beth (father of E.W. Beth). I employed this same method in “Conquest of the Plane” (2011). A more traditional and in my view less transparant presentation as mostly algebra is by J. van de Craats, here, who also doesn’t fully explain (*), see question 1.7 on p4 and the answer on p71.

PM 6. Rotation in 2D can be modeled by a 2 x 2 matrix, see a bit of theory: step1 and step2. A complex number is equivalent to a matrix, and the multiplication of two complex numbers can be represented as matrix times vector. Hence there is a relation between the number -1 and the matrix H for a half turn.

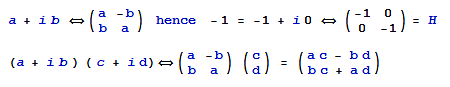Let Q be a quarter turn counterclockwise, then Q 1 = i. A half turn H = Q² = – I, where I is the unit matrix. Then H 1 = -1. A clockwise turn is Q^T, the transpose of Q , and we find Q³ = Q^T. We can find H also as the square of this transpose.

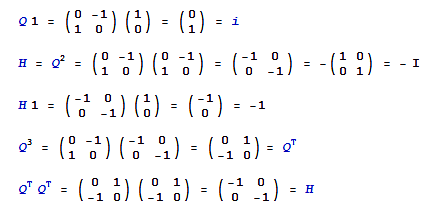The discussion above about H = –H thus can be resolved by the distinction between matrix H and number -1, and we find that actually H = H^T. There remains a point of doubt though. There is an isomorphism between complex numbers and the matrix approach, and thus the explanation of rotation in the complex plane by the use of matrices is rather like begging the question.

Teaching quadratic functions (re-engineered)

My book Elegance with Substance (EWS) (2009, 2015) (pdf online) has the theme that mathematics education requires fundamental re-engineering. Mathematicians are trained to think abstractly and are not trained for the empirical science of didactics. When they meet real life students in class, mathematicians suffer from cognitive dissonance, and resolve this by sticking to traditional ways of teaching, which tradition has not been designed for optimal didactics. In this manner, mathematics education is in shambles for some 5000 years.

EWS documented this with a long list of examples and hence I should not be surprised anymore to find another example. However, I was very surprised to discover the following for the quadratic function. This function is so familiar for at least some 3000 years, and you would expect that mathematicians had optimized its teaching. However, be amazed as well.

A starting point for all approaches

The quadratic function is introduced in all cases by presenting the square of x. The formula is supported by text (explaining what the function does), table (first row for effect y, second row for cause x, namely allow for Δy / Δx), and graph. Write functions with square brackets.

f[x] = x²

Properties are:

• The vertex or turning point can be found at the origin {0, 0}.
• There is symmetry for left and right along the line x = 0 because f[x] = f[-x].
• There are no outcomes f[x] < 0, unless by use of the complex plane with H = i² = -1.
• Also f[x] and –f[x] mirror, but one would say that this requires a coefficient a = -1.
  

Continue re-engineered: a focus on understanding

Changing and moving (transforming and translating) the function gives the basic form.

f[x] = a (x – h)² + v

• The vertex or turning point can be found at {h, v}.
• Coefficient a stretches or squeezes, while a negative value flips or mirrors upside down. Making coefficient a negative turns a convex form into a concave form. (Seen from the origin, concave is hollow or h-shaped, and convex is bulging or b-shaped.)
• The value h shifts the parabola horizontally. For example, x must have a higher value if some positive h is subtracted from it. If h is negative, then the graph moves leftwards.
• The line x = h is also the mirror-axis for left and right.
• The value v shifts the parabola vertically. If v is negative, then it shifts downwards.

A key question for a parabola is where it intersects with the horizontal axis. Even when we want to find the points of intersection with a line y = d, then this only means an adjustment to v’ = v – d. Finding the solution to this quadratic equation is straightforward.

f[x] = a (x – h)² + v = 0

(x – h)² = – v / a

x_1,2 = h ± √(- v / a)

It is easy to check that all solutions must have this symmetric form, since substitution back first eliminates h and then squares the remainder, and reduces to zero. This solution thus also gives the rule:

• When v = 0 then there is a single solution, or it is touching the horizontal axis.
• When – v / a > 0 then there are two solutions.
• When – v / a < 0 then there is no intersection with the horizontal axis. A solution can be found in the complex plane however. There is no need to be squirmish about complex numbers because these would have been discussed before, when discussing the system of co-ordinates (see here).

These graphs show the solutions for f[x] = 1 (x – 0)² + v, for values v = -2, 0, 2. The relevant intersection value is √2 ≈ 1.414…. The complex solution can be found by flipping the function, giving g[x] = -1 (x – 0)² + 2, solve for the intersections, and circle these a quarter turn. Here x_1,2 = ± i √2.

Given the (two) solution(s) x_1,2 = h ± √(- v / a), let us write for ease x = u or x = w, and observe that the function can be written in the factored form: f[x] = a (x – u)(x – w). The vertex or turning point lies in the middle, so that h = (u + w) / 2. Substitution of x = h gives v =  – a (u – w)² / 4.

The basic form can be expanded into the standard (polynomial) form.

f[x] = a (x – h)² + v

= a (x² – 2 h x + h²) + v

= a x² – 2 a h x + a h² + v

f[x] = a x² + b x + c in which b = – 2 a h and c = a h² + v

Thus, conversely, whenever one meets the form f[x] = a x² + b x + c then h and v can be solved as:

h = – b / (2 a)

v = c – a h² = – (b² – 4 a c) / (4 a)

Acknowledgements.

• After re-engineering the above, I knew what to look for, and found this video by MIT graduate Nancy (mathbff) who calls the basic form the “vertex form” but who still has it in 2nd place instead of 1st place. There is also this lesson plan at MARS that mentions the three forms, but their order is standard, factored, basic, and the latter is called “completed square form”. I would rather put basic first and express this in its name. The lesson is what you can directly recognise in each form, which is a fair question, but not the most relevant first question on the graph of the quadratic function.
• The complex graph comes from Norton & Lotto 1984, reproduced by Francis Su et al. here. Su et al. don’t use the basic form whence it is difficult to see how to flip the function and why complex solutions have the real part h and the imaginary part √(- v / a). The complex solution is also mentioned by wikipedia here, but this doesn’t flip the graph and doesn’t explicitly make the quarter turn, so the solution remains mysterious.

The shamble tradition: starting from theory

Mathematicians have developed a theory of polynomials. The traditional approach in teaching the quadratic function is to treat it as a special case of such polynomials.

Thus students are presented with the polynomial format, called the standard form.

f[x] = a x² + b x + c

The standard form is intransparant. Teaching thus proceeds by presenting tricks, only to recover what is already obvious for the basic form.

(1) Students are presented with the quadratic formula and must learn it by heart. This is the fail-safe approach for students without much interest in or understanding of mathematics.

x_1,2 = (-b ± √D) / (2 a) with discriminant D = b² – 4 a c.

The possible solutions are cataloged with D < 0, D = 0 and D > 0.

• It is not clear where D comes from and what it means. (It is only a freak result of the polynomial form.)
• The traditional approach takes so much time in general that there often hasn’t been time to explain about the complex plane, and thus it is often said that D < 0 has no solution rather than that it has a complex solution.

(2) More interested or advanced students can be shown where the quadratic formula comes from. This generates the ritual called derivation of the quadratic formula. There are a number of approaches (wikipedia), but, “surprisingly” the following approach may not be mentioned (not in wikipedia today), and the reason must be that the tradition has lost track of the basic form.

a x² + b x + c = a (x – h)² + v

For x = 0: c = a h² + v hence v = c – a h²

For x ≠ 0: a x² + b x + c = a x² – 2 a h x + a h² + v

b x = – 2 a h x and hence h = – b / (2 a) and substitute this in v again

Subsequently resort to above disucssion, and find x_1,2 = h ± √(- v / a)

Didactic conclusions

Didactic conclusions are:

• The basic form is transparant, provides a clear path to the standard (polynomial) form, and also provides clarity for the return path from the standard form back to the basic form.
• Starting with the standard form is convoluted. It starts from some distant theory about polynomials in general and creates clutter and mystery about solutions. This tradition has lost track of the basic form and thus also requires more intricate solution methods or reliance on memory for the “quadratic formula”.
• Making math opaque for such simple issues puts a heavy burden on more intricate issues.
• Making math opaque for such simple issues also causes a flight into alternative approaches, such as reliance on applications (“realistic mathematics education” (RME)). Interesting applications are here, but my impression is that students will study those applications with more interest once they have mastered the basic form first. The general format for teaching is: (a) psychologically prime notions with a basic example (here the square of x), (b) develop the theory, (c) apply the theory.

PM. Wikipedia is not a didactic environment but a portal. When you want to know what the “quadratic formula” is, then wikipedia presents it, and wikipedia doesn’t give a didactic presentation of the underlying issue. Wikipedia has other entries like on the quadratic equation, but following these links doesn’t generate a didactic exposition. Thus beware: mathematics in wikipedia is created by math students who copy their textbooks.

Examples: two English websites and a Dutch textbook for grade 9 (age 14-15)

A traditional presentation of the quadratic function that “completes the square” without giving the general form is here. Another website is here, and it gives the basic (“vertex”) form somewhere at the end.

A Dutch textbook for grade 9 at subtop-level (“Moderne wiskunde”, HAVO 3ab, together 400 pages, edition 8, 2005) includes the following approach to the quadratic function.

• Ch 3 (some 25 pages): Transformation and translation of functions (linear, quadratic, hyperbolic, powers and roots). It makes sense to review the different functions. However, for the quadratic function only a and c are manipulated. Given above discussion, it would make more sense to discuss each function separately with its transformations and translations.
• Ch 5 (some 25 pages): Factoring polynomials. This is a basic algebraic skill. It is enlightened in the textbook with graphs of rectangles and indeed a parabola. When the treatment of the parabola is as convoluted as it is now, then this order can be understood, for the solution of a quadratic equation can be found by factoring. A more didactic approach however would be to (a) discuss factors using rectangles, (b) discuss the parabola in the re-engineered fashion, and (c) only later practice also on the skill of factoring. The advantage of the re-engineered approach is that we can have text, formula, table and graph in a single review at a much earlier stage, which enhances understanding.
• Ch 8 (some 30 pages): Quadratic formulas. The traditional f[x] = a x² + b x + c with vertex and symmetry, quadratic formula, the use of D, graphical form, and solution of quadratic equations. In the re-engineered approach, this would be integrated in the earlier chapters 3 and 5.
• Ch 9 (some 25 pages): Manipulating more functions: Addition and multiplication of graphs. Periodic formulas. This deepens earlier notions and provides more practice. This might be less needed in the re-engineered approach when issues are transparant.
• Ch 11ab (some 50 pages): Graphs and equations. Intersection of graphs and finding solutions. However, finding the intersection of parabola a x² + b x + c and line b’ x + c’ reduces to a x² + b x + c = b’ x + c’ or solving a x² + (b – b’) x + (c – c’) = 0, which is just solving for another parabola, which has already been discussed. This split chapter only practices earlier notions, which might be less needed when the presentation was transparent enough.

The conclusion is that this textbook provides key ingredients, but in less didactic format and order, such that the textbook resorts to a lot of practice to allow students to replace insight by routine. (Routine should not be called skill when insight is lacking.)

Conclusion

There is scope for re-engineering the didactics of quadratic functions into a much more transparant manner. The focus must be on what is essential to understand (at this level) and on starting from some abstract general theory (relevant for understanding issues at another level).

This re-engineered approach can likely already be used in elementary school. See the other book A child wants nice and no mean numbers (CWNN) (2015) (pdf online).

It remains to be tested whether the re-engineered approach indeed is as transparant as suggested here, and whether pupils would have a fast road to insight and skill and improved attitude. It always are the students themselves who show what works for them.

Referenda tend to be silly and dangerous – see the Brexit

President Obama can do little other than teach, in the last year of his presidency and with a majority opposition. Obama just advised the British to vote for the EU on the Brexit referendum. He is at risk of infringing upon national sovereignty, the very thing that the referendum is about.

The Brexit referendum stay / leave question is, and let me include the FT poll score,

Should the United Kingdom remain a member of the European Union or leave the European Union?
– Remain a member of the European Union [  ] (44%)
– Leave the European Union [  ] (42%)

Leaving the EU still allows various alternatives. If the vote would split over those options, perhaps one better stays. There is no way of knowing. Referenda tend to be silly and dangerous.

• Referenda work only well when there are two options only, with a clear-cut Yes / No answer. This kind of question occurs only by exception.
• Normal issues have more options and grades of grey. With at least three options, there arises the Condorcet paradox. For such issues, there better be representative government, with a Parliament selected by proportional representation (PR), and which Parliaments uses more complex methods for bargaining and voting – see Voting Theory for Democracy.
• The pitfall is that a question might seem to have a clear-cut Yes / No answer while it actually has other options and such grades. Check how the Brexit question masks the other options. It often is an issue of political manipulation to reduce a complex issue to seeming simplicity, and to create a situation such that the political leader who drafts the question might argue to have the backing of the people.
• Referenda belong to populism and not to democracy.

In this case, UK prime minister David Cameron has to overcome a rebellion in his own party and the threat of defection to UKIP. Check this report on Cameron’s bargaining with the EU. Given this bargaining result Cameron now argues for the EU and he hopes to secure peace in his party. It is somewhat curious that the whole of the UK is called to the ballot box to resolve such internal strife, but the same happened in 1975 with Harold Wilson and the Labour Party.

An advantage of the Brexit referendum is that the BBC now had two broadcasts “Europe: Them or Us“, that review the relation of the UK to the EU. It has been awfully nice to see the ghosts of the pasts perform their part in this drama. See also here and youtube. Some key points that struck me were:

• Churchill argued for a united Europe.
• The UK 1975 referendum caused people to complain a decade later: “We voted for a Common Market and later we got something else.”
• Margaret Thatcher started out as a European, supported Europe in 1975, actually initiated and signed the 1986 Single European Act, with the change from a Common Market (with veto power by country) to the (Europe 1992) Single Market (replacing veto power by qualified majority), and whisked it through the UK Parliament without proper discussion about this abolition of national sovereignty. Only later came the 1988 Bruges speech.

The key point for Cameron has been to restore a shadow of that veto power. Britain cannot block others from having an ever closer union, but it has an opt-out:

“Assessment: Mr Cameron has secured a commitment to exempt Britain from “ever closer union” to be written into the treaties. He has also negotiated the inclusion of a “red-card” mechanism, a new power. If 55% of national parliaments agree, they could effectively block or veto a commission proposal. The question is how likely is this “red card” system to be used. A much weaker “yellow card” was only used twice. The red-card mechanism depends crucially on building alliances. The sceptics say it does not come close to winning the UK back control of its own affairs – and Mr Cameron is set to announce further measures which he claims will put the sovereignty of the Westminster Parliament “beyond doubt”.” (BBC Feb 20 2016)

Some points that I missed in these two “Europe: Them or Us” broadcasts:

• There is no recognition for Bernard Connolly whose The Rotten Heart of Europe helped the British to stay out of the euro and to keep the pound. There is still room for a better approach to the notion of an optimal currency area.
• There is little clarity about what the economic discussion really has been about. “Economic union” and “political union” are vague words, and it seems relatively easy to make a political speech or TV broadcast with these. Details matter however. Details help to keep out the ideologues. It is said that Britain has the best economists (Marshall, Keynes, Hicks) but Germany the best economy. Margaret Thatcher would have been much more effective when she had proposed good economics rather than banging the handbag. The relation of the UK to the EU would have been far better had the UK shown better economic analysis and an economy to prove it. Thatcher came to power during a time of stagflation when economists were in disarray and neoliberalism seemed the only way out. This neoliberalism however contributed to the global financial crisis and the economic crisis of 2007+. See my analysis since 1990. Of the core issue, a recent turn is the myth about German decentralised labour market bargaining. Britain has an impact on the European economy via the City and its banks (a fair reason to stay in), but why doesn’t Britain have more impact ?
• Democracy in the UK suffers from district representation (DR), and it would be better to have proportional representation (PR). There is too little awareness in the UK that much of their political mayhem is caused by their rather unresponsive electoral system. See the comparison of Holland and the UK, and see how Nick Clegg shot his own foot (and destroyed the LibDems).

PM. After writing this, I discovered this review of “Europe: Them or Us” by Sean O’Grady and he says much of the same thing.

The recent Dutch referendum on the Association treaty with the Ukraine is another example of how referenda can be silly and dangerous. I voted against that treaty because of the military section hat would involve the EU in helping secure the Ukrainian borders, which would effectively move NATO’s borders eastward. Government propaganda did not pay much attention to the military section and emphasized the section on free trade. Even there the propaganda didn’t draw the parallel with the economic collapse in East Germany (DDR) when it was merged with West Germany (BRD). In this case, representative democracy failed, for it created this Association treaty, and the Dutch referendum was a freak event that might actually do some good. It still confirms that referenda tend to be silly and dangerous, since the proper answer would have been a better informed discussion in Parliament, notably by having (a) an Economic Supreme Court, (b) annual elections.

Thanks to Jos Collignon for permission to reproduce this

John Quiggin’s amateur political analysis

Last February, fellow economist John Quiggin tried to make sense of political developments by relating those to the economic crisis of 2007+ a.k.a. the Global Financial Crisis (GFC). Quiggin warned about his “amateur political analysis” and proceeded to identify a “three party system“: with leftism, neoliberalism and tribalism (see his definitions). The neoliberals are soft (“reforming” the welfare state) or tough (abolishing it). Dutch readers may check the column by Wouter de Been which alerted me to this, and who argued: “It’s still the economy, stupid.”

A first comment is that Quiggin actually has four groups, namely leftism (Bernie Sanders), soft neoliberals (Hillary Clinton), hard neoliberals (Donald Trump) and tribalism (Ted Cruz). See the diagram below.

A second comment is that Quiggin uses the economic term “neoliberalism” as a political label. However, economics is a tool and not an objective. Instead we should categorize politics by values, such as (in-) equality and freedom. It must be admitted that economics has much influence on political discussion but it remains necessary to distinguish ends and means.

• As discussed before, Emmanuel Todd distinguishes the stable categories of equality / inequality and authoritarian / liberal. A common distinction is between the political “left” and “right”, but this distinction is vague, and it is more informative to distinguish Todd’s two dimensions.
• For Trump, the label rather isn’t “liberalism” but “neoliberalism” (“freedom”). Trump pursues more freedom but does so in an authoritarian manner. Over time his manner could be more important than his stated goals and then he would shift down.

Quiggin holds that there is instability because of the Condorcet paradox and other reasons. A third comment is that these four can actually be arranged on a left-to-right line and then fit the Duncan Black single-peakedness and the median voter theorem.

• In the diagram, the conceptual gap between Sanders and Trump is rather large, and they are only comparable in radicalism. Clinton and Cruz are closer on caution and conservatism.
• In Europe, we might perceive of a coalition that excludes the inequality & authoritarian group and includes the others on liberty, equality and fraternity (in the colour map: exclude green and include the others). This coalition might work if there is gradual change and no French Revolution.

A fourth comment however is that there better be electoral reform, such that parties can collaborate on issues rather than fight about ideology.

Other charts on political views

Sanders and Trump seem to score higher on their radicalism than on clarity about a position on the scale from authoritarian to liberalism / freedom / neoliberalism. We could include a third dimension of the attitude towards change. There is a range from conservatism to radical adaptation. The term “conservative” itself is ambiguous: it may mean that one wants to maintain the status quo (e.g. with current liberal properties), but it may also mean that one wants to return to some ideal past (reactionary, e.g. with king and aristocracy (billionaires)).

A fifth comment thus is to maintain caution on these dimensions.

The Nolan chart has the axes of economic freedom (low to high) and personal freedom (low to high). This compares to the chart above, when we replace equality / inequality with economic freedom, and replace authoritarian / liberalism with personal freedom. The Nolan chart however again confuses political values with economics as a tool. There is also the problem of balancing opposite effects.

• A minimum wage reduces the economic freedom of the entrepreneur and the outsider unemployed, but enhances the economic freedom (bargaining position, income) of the insider employees. See DRGTPE for a better approach to the economics of the minimum wage. This is economics and not an issue of political values, though politics are relevant when deciding what policy to adopt.
• One might presume a natural state and then hold that any measure that is to the disadvantage of someone counts as the reduction of economic freedom, even when it would advantage others. However, there is no clear specification of such a natural state. (Todd’s scheme identifies at least four types of family structure.)

A classification of Dutch political parties by Andre Krouwel (“kieskompas“) still uses the political left-right distinction, but this distinction has been based upon programme details and thus might still be relevant.

The lifestyle consultancy firm Motivaction identifies eight groups in Dutch society, from traditionals to post-modern hedonists. Potentially these link up to political parties.

Return to economics

I tend to agree with Quiggin:

“But the more fundamental problem is that none of the competing forces has an obviously compelling solution to the problems we face. Neoliberalism has manifestly failed to deliver the prosperity promised by triumphalists like Thomas Friedman in the 1990s. Tribalism is already a lost cause, given the massive migrations that have already taken place, and can at most be slowed in the future. The left needs to rebuild institutions and policies that have been in retreat for decades.”

The true problem is one for economic analysis. The derived problem for the political leaders and parties and their voters is to select which economic advisors to listen to. The sixth comment is that there is censorship of economic science since 1990 by the directorate of the Dutch Central Planning Bureau (CPB). Governments didn’t get proper advice, and the economic crisis of 2007+ a.k.a. GFC is evidence of this. Boycott Holland till this censorship is solved. See the About page. What the censored analysis fully is can only be seen after the censorship has been lifted of course.

Common sense rejection of Rapoport’s four waves of terrorism

I am no expert on terrorism and wonder whether the supposed experts aren’t either.

Dutch historian and “expert on terrorism” Beatrice de Graaf gave a lecture on Dutch TV on March 11 (or see Utrecht University) about David Rapoport‘s four waves of terrorism (his original article).

Her main message was that people might find some comfort in the idea that waves die out. March 22 saw the bombs in Brussels.

This theory of four waves of terrorism appears to be rather silly. Below gives my common sense rejection.

De Graaf is not the only academic who regards the theory of the four waves as serious. The West is vulnerable to terrorism when its “experts on terrorism” are academics lost in theory. It is okay to sooth people not to worry too much, but intellectuals should present effective approaches rather than fairy tales.

The so-called “four waves”

Jeffrey Kaplan summarizes (and then proceeds in adding his own fifth wave) (while Dutch readers can check Edwin Ruis’s review of March 13):

“Rapoport’s theory, first published on the web before finally finding a home in a printed anthology, posited four distinct waves of modern terrorism (anarchist, nationalist, 1960s leftist, and the current religious wave). Each wave had a precipitating event, lasted about 40 years before receding, and, with some overlap, faded as another wave rose to take center stage. Most terrorist groups would gradually disappear, a few (the Irish Republican Army for example) proved more durable. Rapoport’s theory was elegant, simple, inclusive, and had a high degree of explanatory power. In short, it provides a good academic model.” (Kaplan 2008).

Jeffrey D. Simon holds (and wonders about a fifth wave too):

“David Rapoport’s “The Four Waves of Modern Terrorism” is one of the most important pieces ever written in the vast literature on terrorism (Rapoport 2004).  What Rapoport did in his classic study was take the complex phenomenon of terrorism and put it in a historical context that not only explained different periods of international terrorism, but also set forth theories and concepts that can be used to attempt to anticipate the future of terrorism.  That is no easy task.  There haven’t been many assessments and articles written about Rapoprt’s “Four Waves” theory, although this volume of papers initiates a discourse about his important thesis (See Thompson and Rasler, this volume).  Despite the numbers of scholars, policymakers, and others who have joined the field of terrorism studies after the 9/11 attacks, there does not appear to be a great deal of interest in the history of terrorism.  In today’s instant access and information-overload society, we are inundated with analyses of current affairs but pay scant attention to what we may learn from what has transpired in the past.” (J.D. Simon on the Lone Wolf, likely 2010)

I googled to find some criticism, but didn’t see much, though perhaps I didn’t google well. I noticed a critical text by Ericka Durgahee. I didn’t have time to look into this, and the following are my own common sense short remarks.

The anarchists 1880-1920

The dynasties of Hohenzollern, Romanov and Habsburg collapsed. Perhaps the anarchists didn’t really win because we don’t have anarchy now, but those anarchists were replaced by communists and fascists, and we ended up with two world wars, which isn’t quite “die out”.

Anti-colonialism 1920-1960

The anti-colonialists won. Winning isn’t quite “die out”.

Leftists 1960-1989

Leftism became impopular because of the Great Stagflation (unfavourable unemployment and inflation) and the collapse of the Berlin Wall. Young radicals were more motivated by Ronald Reagan and Margaret Thatcher.

In Germany, the police managed to isolate the Rote Armee Fraktion (RAF). In another article, Beatrice de Graaf explains how the Dutch radicals (Rode Jeugd, Krakersbeweging) lost their motivation by incompetence of the Dutch police. The Dutch police intended to adopt the tough German approach, but mismanaged this, and both radicals and the general population got the impression of an atmosphere of tolerance and dialogue. In that atmosphere, potential supporters saw no need for radicalisation, and radicals had the example of the dead-end street in Germany.

These events rather concern the transformation of European society after World War 2. There are pockets of terrorism, but there doesn’t seem much difference between RAF and other groups like IRA and ETA: except that each group requires specific attention for its idiosyncracies.

Religious terrorism 1979-now

Religious violence is of all times. There is no reason to predict that it will pass. This is no wave.

Alternative approach

Terrorists tend to be higher educated who are frustrated w.r.t. opportunities in society. They may feel sympathy with the unprivileged. They may adopt any ideology to recruit others in the resistance against the establishment. To counter this, one must look at society as a whole, create fair opportunity, and encourage people to participate. My own work contains aspects that are key to reduce terrorism.

• Create a social welfare state that works. See DRGTPE.
• Make democracy work. See VTFD.
• Provide for good education, e.g. re-engineer mathematics. See EWS.
• Let people learn how to deal with the human capacity for abstraction. See SMOJ.

Beatrice de Graaf, soothing Dutch viewers that a wave of terrorism dies out

 

Blunder or deviousness ?

continued from the former entry of April 4

The turnout of 32% at the April 6 2016 Dutch Referendum on the EU-Ukraine Association Agreement does not seem convincing. The 61% No vote seems impressive over the 38% Yes vote and 1% blanks, but the low turnout gives it little weight. (PM. The electorate are 13 million voters. Turnout was 4.2 million. For the treaty were 1.6 million and against the treaty were 2.5 million.)

This advisory referendum is labelled “valid” because it passed the ceiling of 30%, but the margin is so low that Mark Rutte and his government might feel excused to still ratify the treaty anyhow.

It would take only 12% to switch the No majority into a Yes majority.

Potentially, the No voters were most motivated to turn up, and the Yes voters potentially stayed at home because: (a) the referendum was advisory only, and they have reason to believe that the government would ratify the treaty anyway, (b) the referendum would be invalid when the ceiling of 30% turnout would not be reached, (c) they might believe that they were the real majority so that the outcome would be Yes anyway. Perhaps a 12% higher turnout would only have come from Yes voters.

Thus the EU might blame Mark Rutte and his government for not having tried hard enough to increase the turnout that might have caused that switch in outcome.

However, the earlier poll by Maurice the Hond suggests that a full turnout would show 53% No. We can find this figure by weighing the views of the polled votes per party with the current polled seats per party. Indeed, De Hond also concludes that the No vote would never fall below 50%. However, it is hazy what a full turnout would be. There hardly ever is 100%. Let us take the 75% turnout of the last general elections in 2012.

Assuming proportional change between these two data points {.32, .61} and {.75, .53} gives us the following sloping line that drops to 50% at 90% turnout.

Referendum result at 32% and potential at 75%

Conclusions are:

• With the {.75, .53} poll data point included, the referendum result is more impressive than it at first seems. Apparently the Yes vote indeed had a losing uphill battle.
• Mark Rutte and his goverment should have tried harder to inform the electorate about the pro’s and con’s of the treaty, if they really thought that more information would have resulted in both a higher turnout and a switch to more Yes votes.
• Mark Rutte and his goverment might not have put in this effort, since the referendum was only advisory and might not have reached the 30% ceiling.

On the sight of it, Mark Rutte and his government have blundered.

It may also be plain old Dutch deviousness: with a ploy to play into Putin’s paranoia, and a scheme to prevent a casus belli. Remember the movie “Being there“.

Memo by Kasparov for Putin on the EU – Ukraine Association

Yesterday I had my regular lunch with Vladimir Putin, President of the Russian Federation.

We mostly talked on how the oil price inflates corruption, and we focused on which sport he wants to enter in the next Olympic games: judo, swimming, horseback riding, shooting, or some other sport that he hasn’t shown us yet that he excels in. We curtly discussed the Dutch referendum of next Wednesday April 6 2016 on the EU – Ukraine Association Agreement.

TC: “Vlad, you have been remarkably silent on this Dutch referendum. I had expected to see the Russian Ambassador on Dutch TV campaigning for a No, but I haven’t seen him.”

VP: “Well, I want to invade the Eastern Ukraine this Spring, and this treaty is a welcome cause of war. I would be dismayed when the Dutch people would say No to the treaty and thus block it. Besides, I have asked the Ambassador to undergo a sex change operation to be more agreeable to the Dutch gays.”

TC: “When you ask the Dutch to say No, they will likely become obstinate and vote Yes. Then you have your casus belli and can also claim that you have done your best to prevent it. Or am I trying to out-smart you ?”

VP: “That would also be seen as meddling in internal national affairs. Russia doesn’t meddle. We spy or invade. I trust that the Dutch government will ratify the treaty, even when the population says No. I have promised your prime minister Mark Rutte a good job at Gazprom later on, and he seemed very happy to sit up and eat the cookie.”

TC: “Thus by July 2016 Russia will have occupied the region East of the Dnieper, and Kiev will be divided by a Wall. The EU can have its treaty with the West, and can start trying to feel happy with the mess they created.”

VP: “There is something very alluring to a permanent stalemate, like the division between North and South Korea. A permanent state of war will be very invigorating to Russia’s youth.”

TC: “Ah yes, I understand what you are thinking. Marches and parades. Battle songs. Soccer stadiums filled with ballet dancers in clockwork performances. Adrenalin is better dan meldonium. The European Union will not understand what hit them. You are brilliant and a real father for Russia.”

Vlad turned to me with a surprisingly modest expression: “Don’t give me credit. I got the idea from Garry Kasparov. Let me give you his Memo. I don’t mind when you publish it and let your Dutch friends read it too. Kasparov always loses from me in chess or politics, and he is a lousy house cleaner and waiter, but his Memo deserves some credit.”

I read the Memo in the plane, and was happy that there was plenty of Stolichnaya for the remaining three hours of the flight back home.

Memo by Garry Kasparov for Vladimir Putin, April 1 2016

Normally I try for a straight argument and end up into convolutions. Now I won’t even try.

The EU – Ukraine Association Agreement (henceforth treaty) text is here and on wikipedia (or in Dutch here and here and wiki). The wikipedia article shows that the treaty is ratified in all countries except that Holland has a referendum on April 6 2016 that might still block it.

Wikipedia actually has an article on this Dutch referendum. The Dutch referendum allows citizens only to advise the government. The government might still choose its own way – which likely is a Yes. Hence we are mostly discussing chimeras.

My main concern is the risk of war, whence I am against the treaty as it stands. Article 7 on Foreign and security policy involves the EU in a “timely and coherent manner” in the defence of Ukrainean sovereignty. The Ukraine might claim that the Crimea has been stolen by Russia, must be returned, and that the EU is legally obliged to help to get it back in “timely and coherent manner” . This is Article 7 with my emphasis:

1.   The Parties shall intensify their dialogue and cooperation and promote gradual convergence in the area of foreign and security policy, including the Common Security and Defence Policy (CSDP), and shall address in particular issues of conflict prevention and crisis management, regional stability, disarmament, non-proliferation, arms control and arms export control as well as enhanced mutually-beneficial dialogue in the field of space. Cooperation will be based on common values and mutual interests, and shall aim at increasing policy convergence and effectiveness, and promoting joint policy planning. To this end, the Parties shall make use of bilateral, international and regional fora.

2.   Ukraine, the EU and the Member States reaffirm their commitment to the principles of respect for independence, sovereignty, territorial integrity and inviolability of borders, as established in the UN Charter and the Helsinki Final Act of 1975 of the Conference on Security and Cooperation in Europe, and to promoting these principles in bilateral and multilateral relations.

3.   The Parties shall address in a timely and coherent manner the challenges to these principles at all appropriate levels of the political dialogue provided for in this Agreement, including at ministerial level.

Professor Richard Sakwa (page at Kent) advises a No. His book is here and reviews are here and here. He agrees that the Ukraine already is a sovereign nation and has the right to engage into the current treaty with the EU. The EU has the right to engage into such a treaty too. However, it would not be wise to do so. The EU is sleepwalking again, like the sleepwalkers of 1914-1918.

Sakwa was on Dutch TV on March 20 2016 explaining – in English with Dutch subtitles (minute 41) – that the EU should look at the whole region, including the position of Russia. He was challenged by the Dutch vice-prime-minister Lodewijk Asscher with the argument that including Russia in the picture would violate the notion that the Ukraine is a sovereign nation. Asscher is a lawyer and wields a legal argument in a discussion on geopolitics and war. When Hitler invaded Holland, Asscher would say that this was illegal. Asscher has been doing all kinds of silly things but he has a quiet and soft presentation that Dutch people seem to take for wisdom.

Thus the reasoning is:

• There should be a peace agreement with both Russia and Ukraine.
• There should be a trade agreement with both Russia and Ukraine.
• This current Association Agreement does not satisfy these conditions. In fact, it reduces the freedom of the Ukraine to enter into trade agreements with Russia. The Ukraine becomes the outer border of the European trade area. Trade between the Ukraine and Russia will be hit, and this will cause unemployment in the Ukraine, similarly to the unemployment that occurred in Eastern Germany after the fall of the Berlin Wall (see here).
• The EU should stop the policy that association with the EU means association with NATO.
• The EU should use “Europe” as a term in geography and not as synonymous with EU.
• Hence No to the current treaty.

Richard Sakwa on Dutch TV (March 20 2016, minute 41)

PM 1. Arno Wellens (in Dutch) finds it curious that Asscher was not at the discussion table, and was asked for his opinion while sitting in the audience. Wellens suggests that Sakwa anticipated a 20 minute focus on his analysis, but was surprised to find himself in a discussion with the vice-prime-minister. Perhaps this is the case. Still, it is useful to see the clash between geopolitics (Sakwa) and legalism (Asscher).

PM 2. Another English source is Mark Almond at Oxford, but perhaps a bit less outspoken as Sakwa.

PM 3. For Dutch viewers there is a nice discussion of March 27 between Jeroen Dijsselbloem (Yes) and Arjo Klamer (No). Klamer’s main concern is that the Ukraine has too much corruption, so that the EU’s neoliberal policies will benefit the oligarchs and be disastrous for the common people. This is partly correct. It is strange that Klamer doesn’t give a better economic analysis, but see here (in Dutch).

PM 4. There is some information on a EUR 11 bn Ukraine state building project financed by the EU. This is about EUR 250 per Ukrainean, or one-time 12.5% of the annual GDP per capita of EUR 2000. We may guess where this money is going to land. Perhaps it is an acceptable bribe to get better law and police in the long term. That said, there is still the issue of war. It would be foolish to pay a bribe to get involved in fighting.