Simpson’s paradox, and how to correct it
Econometrics researches the economy, using mathematical models and statistical data. For me as an econometrician the important relations are given by the causality in economics. The observed causality is put into the model. The model explains what we think that the causal chains are. Statistics can only give correlation. Thus, there is a tension between what is required for economic analysis and what statistics can provide. Different models may meet with the same data, which means that they would be observationally equivalent, yet, they would still be different models with different assumptions on causality.
Judea Pearl in his wonderful book “Causality” (1ste edition 2000, my copy 2007) of which there now is a 2nd edition, took issue with statistics, and looked for a way to get from correlation to causality. His suggestion is the “do”-statement. I am still pondering about this. For now I tend to regard it as manipulating in models with endogeneity and exogeneity of variables. Please allow me my pondering: some issues require time. See here for an earlier suggestion on causality, one on the counterfactual, and one on confounding. Some earlier papers on the 2 x 2 x 2 case are here. Today I want to look a bit at Simpson’s paradox with an eye on education.
The order of presentation in tables
In graphs, the horizontal x axis gives the cause and the vertical y axis gives the effect. For the derivative we look at dy / dx. Thus in numerical tables we better put the y in the top row and the x in the bottom row.
For 2 x 2 tables the lowest row is the sum of the rows above. Since this lowest row better be the cause, we thus better put the cause in vertical columns and the effect in horizontal rows. This seems a bit of a paradox, but see the presentation below.
(This is similar to when we have the true state (disease) (gold standard) vertically and the test statistic (test) in the rows, when we determine the sensitivity and specificity of the test. Check the wikipedia “worked example“, since the main theory is transposed.)
Pearl (2013) “Understanding Simpson’s Paradox” (technical report R-414) has a transposed table. It is better to transpose back. He also mentions the combined group first but it seems better to put this at the end. (PM. A recent discussion by Pearl on Simpson’s paradox is here.)
Pearl’s data example (transposed)
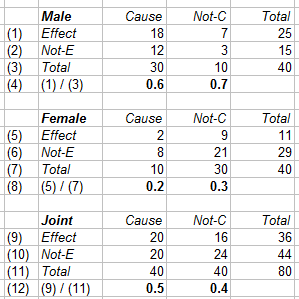
The following are the data from Pearl (2013), the appendix, figure 4, page 10. The data are the count of the individuals involved. Both men and women are treated (cause) or not, and they recover (effect) or not. Since this is a controlled trial, we do not need to look at prevalence and such.
When we divide the effect (row 1) by the total (row 3) then we get the recovery rates (row 4). We do this for the men, women and joint (combined, pooled) data. We find the paradoxical situation:
- For the men, the treatment causes reduced recovery (0.6 < 0.7).
- For the women, the treatment causes reduced recovery (0.2 < 0.3).
- For all combined, the treatment causes improved recovery (0.5 > 0. 4).
More models that are statistically equivalent
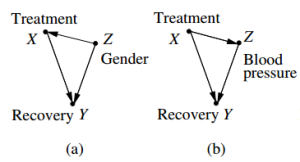
We may arrange issues in “cause” and “effect”, but the real relations are determined by reality. Data like these might be available for various models. Pearl (2013) figure 1 mentions more models, but let us consider cases (a) and (b). In the above we have been assuming model (a) on the left, with a path from cause X to effect Y, in which variable Z (gender) is causally independent. Above data table however would also fit the format of model (b), in which variable Z (blood pressure) would not be independent, and might be confounding issues.
Perhaps the gender is actually confounding the situation in above table too ? The result of the table is so strange that we perhaps must revise our ideas about the causal relations that we have been assuming.
Pearl’s condition for causality
Pearl’s condition for causality is that “the drug has no effect on gender”, see p10 and his formula (7) (with there F rather than here Z). The above data show that there is an effect, or, when we e.g. look at the women, that Pr[Female | Cause] and Pr[Female | No cause] are different, and thus differ from the marginal probability Pr[Female].
In the table above, we compare line (7) of all women with line (11) of all patients. The women are only 25% of all treated patients and 75% of all untreated ones. Perhaps the treatment has no effect on gender, but the data would suggest otherwise.
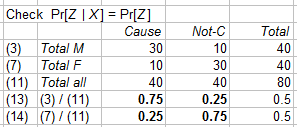
It would be sufficient (not necessary) to adjust the subgroup sizes, such that there is “equal representation”. NB. Pearl refers here to the “sure thing principle” apparently formulated by Savage 1954, which condition doesn’t modify the distribution. For us, the condition and proof of equal representation has another relevance now.
Application of the condition gives a correction
Since this is a controlled trial, we can adapt by including more patients, such that the numbers in the different subgroups (rows (3) and (7), below in red) are equal. This involves 40 more patients, namely 20 men in the non-treatment group and 20 women in the treatment group. This generates the following table.
For ease, it is assumed that the conditional probabilities of the subgroups – thus rows (4) and (8) – remain the same, and that the new patients are distributed accordingly. Of course, they might deviate from this, but then we have better data anyway.
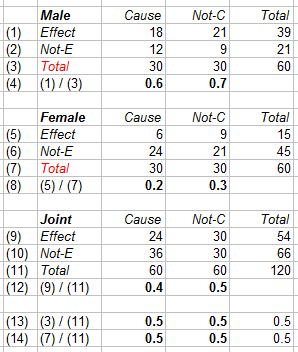
The consequence of including adequate numbers of patients in the subgroups is:
- Row (13) now shows that Pr[Z | C] = Pr[Z | Not-C ] = Pr[Z], for Z = M or F.
- As the treatment is harmful in both subgroups, it also is harmful for the pooled group.
Intermediate conclusion
Obviously, when the original data already allow an estimate of the harmful effect, it would not be ethical to subject 20 more women to the treatment – while it might be easy to find 20 more men who don’t have the treatment. Thus, it suffices to use the above as a statistical correction only. If we assume the same conditional probabilities w.r.t. the cause-effect relation in the subgroups, then the second table gives the counterfactual as if the subgroups had the same number of patients. There would be no occurrence of the Simpson paradox.
This counterfactual would also hold in cases when we cannot simply adjust the group sizes, like the classic case of admissions of students to Berkeley.
While the causality that the drug has no effect on gender is quite clear, the situation is less obvious w.r.t. the issue on blood pressure. In this case it might not be possible to get equal numbers in the subgroups. Not for ethical reasons but because people react differently on the treatment. This case would require a separate discussion, for the causality clearly is different.
Educational software on Simpson’s paradox
There are some sites for a first encounter with Simpson’s paradox.
A common plot is labelled Baker – Kramer 2001 but earlier were Jeon – Chung – Bae 1987. This plot keeps the number of men and women and the conditional probabilities the same, and allows only variation over the enrollments in the subgroups. This nicely shows the composition effect. The condition of equal percentages per subgroup works, but there are also other combinations that avoid Simpson’s paradox. But of course, Pearl is interested in causality, and not the mere statistical effect of composition.
The most insightful plot seems to be from vudlab. It has upward sloping lines rather than downward sloping ones, which somewhat seems easier to follow. There is a (seemingly) continuous slider, it rounds the person counts, and it has a graphic for the percentages that makes it easier to focus on those.
Kady Schneiter has various applets on statistics, of which this one on Simpson’s paradox. I agree with her discussion (Journal of Statistics Education 2013) that an example with pets (cats and dogs) lowers the barrier for understanding. Perhaps we should not use the size of the pet (small or large) but still gender. The plot uses downward sloping lines and has an unfortunate lag in the display of the light blue dot. (This might be dogs, but we can also compare with the Berkeley case in vudlab.)
The Wolfram Demonstrations by (1) Heiner & Wagon and (2) Brodie provide different formats that may come into use too. The advantage of the latter is that you can put in your own numbers.
This discussion by Andrew Gelman caused me to google on these displays.
Alexander Bogomolny has a fine vector display but there is no link to causality (yet).
Robert Banis has some data from the original Berkeley study, and excel sheets using them.
Some ten years ago there would have been more references to excel sheets indeed, with the need for students to do some editing themselves. The educational attention apparently shifts to applets with sliders. For those with still an interest in excel, the sheet with above tables is here: 2017-01-28-data-from-pearl-2000.
And of course there is wikipedia (a portal, no source). (Students from MIT are copying their textbooks into wikipedia, whence the portal becomes unreadable for the common reader. It definitely cannot be used as an educational source.)
Conclusion
This sets the stage for another kind of discussion in the next weblog entry.