Pyramids and the meter

Belgian television showed the film The Revelation of the Pyramids. It contains an intriguing suggestion for a mathematical relationship. Let us debunk it, though keep the intrigue.

I have three reasons to look into this. The first reason is the earlier weblog on the use of ‘archi’ Θ = 2 π = 6.283185307… rather than π as the key mathematical concept for the measurement of the circle. Other people suggest ‘tau’ τ but that looks too much like the radius r and thus will cause much confusion in the classroom. The second reason is the earlier weblog on the mathematics of Jesus. Since the holy family fled to Egypt there is ample reason to look what was happening there. The third reason is that the film suggests that there was an ancient advanced civilisation. Since we may all be disappointed about how we ourselves are doing as a civilisation, it would be great when we could discover that others in the past have been doing much better.

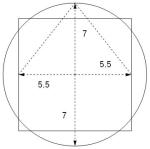
We will also use ‘phi’ φ = 1.618033989… or the golden ratio. This has the property that φ² = 1 + φ, or alternatively that φ = 1 / φ + 1. It allows a particular interesting application of the Pythagorean Theorem. A right angled triangle with base a = 1 and height b = √φ generates a hypothenusa of c = √ (a² + b²) = √(1 + φ) = √ φ² = φ. The associated square has the surface φ², and by using a circle of radius φ we can find that same value in the length of the interval 1 + φ. It appears that these dimensions have been used in the pyramid of Cheops. To measure length the Egyptians used the ell or the (royal) cubit of approximately 0.5236 meters (wikipedia: between 52.3 and 52.9 cm). The pyramid of Cheops has a height of 280 cubits and a full base of 440 cubits. That shape however consists of two right angled triangles. The proper triangle has a base of 220 cubits. The ratio is 280 / 220 = 14 / 11. It so happens that 11 * √φ = 13.99221614… ≈ 14. Thus the Egyptians chose a ratio in integer numbers that closely matches the real value of the golden ratio.

The film The Revelation of the Pyramids now presents the startling equation:

π = 0.5236 + φ²    or      π = cubit + φ²

Startling about this is that π and φ are pure numbers while the length of the cubit only makes sense when everything is expressed by using the meter as the standard length. The pure numbers π and φ come about as ratio’s and thus by dividing lengths so that they do not depend upon any choice of measurement standard. But the value of the cubit changes if we switch from meters to feet and inches.

A first step is to check for accuracy. We find that π – φ² = 0.5235586648… Thus the relation only holds by approximation, though the accuracy is eery.

A second step is to divide both sides by the cubit, or rather by the pure value π – φ². Then we find:

π / (π – φ²) = 1 + φ² / (π – φ²)

6.000459671… = 1 + 5.000459671…

There we are.

Do you see it ? Well, it took me some moments to find the proper sequence of explaning, so let us follow these steps.

A major point is that the use of π has been playing a misleading role in this analysis. It gives only a half circle and it is much better to use Θ and the whole circle.

The first point is the surprise that φ² / (π – φ²) = 5.000459671… Reworked, we get:

φ² / Θ ≈ 5 / 12

What is to say about that ? Well, it apparently is a mathematical property, like 11 * √φ ≈ 14. Sometimes mathematical numbers with complex properties and long decimal expansions can get close to ratio’s of specific integer values. This may be surprising, but it is a mathematical surprise. It cannot be a base for concluding that the ancient Egyptians knew about the decimal expansions of these numbers and their particular ratio. Once you decide to build a pyramid using the ratio of 14 / 11 since it is pleasing to the eye and with structural stability, then you are stuck with the implied mathematics, but that does not imply that you know more about the implied mathematics.

Secondly, let us assume that the Egyptians had their ell or cubit as an arbitrary length (based upon the human body). They also divided the year in 12 months and day and night in 12 hours each. Thus for them it makes sense to measure the circumference of a circle by 12 cubits, like we still do in our clocks. Of these 12 pieces of a pie, six can be allocated to π, five to φ², and then one remains (all with a proportionality factor).

A small problem in this discussion is that the Egyptians might use either flexible ropes (circle) or rigid yardsticks (polygon). Let us assume flexible ropes (circle) first, as they have been nicknamed ‘rope-stretchers’. (See the appendix for approximation by a polygon.)

The radius r of that circle follows from Θ r ≈ 12 cubit, giving r ≈ 1.909859317… cubit ≈ 1.91 cubit. For the Egyptians there was nothing special about that number for that radius. The film shows that the capstone of the pyramid would have this side. That is not inconceivable given this geometry. (If the Egyptians had Θ ≈ 44 / 7 from π ≈ 22 / 7 then r ≈ 12 / Θ cubit = 12 * 7 / 44 cubit = 21 / 11 cubit = 1.90909 cubit. For them still no special value.)

It is only for us, who have adopted the meter (rather than feet and inches), that a sense of wonder arises. For r ≈ 1.909859317… cubit = 1.909859317.. * 0.5236 = 1.000002338… meters ! Alternatively put, if we take a circle with radius 1 meter then the division of the circumference by 12 gives us the Egyptian (royal) unit of measurement, namely via Θ r = 12 cubit or one cubit = Θ / 12 = 0.5235987756…. This uses the arcs rather than the sides of the polygon, and presumes that the flexible rope subsequently is transferred to a yardstick. (For the polygon, see the appendix.)

To understand what is happening here requires us to look into the history about the selection of the meter as the European standard of measurement. Officially, the French Academy decided in 1791 that a meter was to be one ten-millionth of the distance from the Earth’s equator to the North Pole (at sea level) (wikipedia). The expedition by Napoleon to Egypt took place in 1798-1801, thus later, and the results of the new Egyptology will not have been available immediately. From this we may tend to infer that the ancient Egyptians knew about the size of the Earth and reasoned like the French. It seems more reasonable to think differently. To start with, it is already curious to take something that is difficult to measure, such as the distance from the Earth’s equator to the North Pole, to define a standard. It seems more reasonable to assume that there were already circulating measures and that the story about the equator was only an embellishment. Apparently the circle with a circumference of 12 ells had been surviving over the ages and still made it into the discussion.

But the film then should be about what happened in France and not about mysteries in ancient Egypt.

NB. There is ample discussion about the measurements of the pyramid. The top is missing so we can only guess what the Egyptians intended. See the original Petrie measurements (base 9068 and height 5776 +/- 7 inches) and this discussion with drawings. Indeed, if the base is 220 cubits and the Egyptians had a precise estimate of  √φ then the height would be 279.8443229 cubits, which is only a 0.06% of the whole height or one finger of a cubit short of 280. Because of this uncertainty, we cannot infer on these grounds that the Egyptians didn’t have a precise estimate of φ. It are other documents that show us that there were severe limits to their number system. We can neither infer that they were aware of the implication that φ² = 1 + φ, We can observe however that they used geometry and architecture that closely matches these results. See the website by Gary Meisner for how you can create your own golden ratio paper pyramid.

PM. Sir Flinders Petrie (1853-1942) suggests that the basic inspiration lies in the circle rather than in the golden ratio. A circle with radius 7 has a circumference of 7 Θ ≈ 7 * 44 / 7 = 44, using the approximation π ≈ 22 / 7. This 44 gives a square with sides 11. A circle with radius 7 has the circumference of a square with sides 11.  Thus we find the numbers 14 and 11 again.

The argument then is that the Great Pyramid expresses Θ ≈ 4 * 440 / 280 = 44 / 7, and that the golden ratio is only a by-product. If this is the case then this knowledge about Θ has been kept secret or has been lost since later documents apparently don’t mention it. It is a bit curious how that knowledge can get lost when that very same pyramid is standing in front of you. Mankind however has achieved greater mysteries. Note that there is no quick transformation into φ² / Θ ≈ 5 / 12. Via Pythagoras φ² ≈ 1 + (14 / 11)² = 317 / 121 and now φ² ≈ 5 / 12 * 44 / 7 = 55 / 21. For us these are approximations only but for the Egyptians it sufficed that the construction worked. The Petrie approach to start with the circle and 14 / 11 ratio seems simplest indeed. Still, the builders will not have been insensitive to the lure of the golden ratio, and it is remarkable that they have hit upon this very shape.

Appendix

We can also assume that they did not use flexible ropes but rigid yardsticks to lay out a polygon with circumference of 12 cubits, and imagined it enclosed by a circle. We can calculate the sine of a half slice, with Sin[angle] = h / r.  A half slice has h = 0.5236 / 2 and the associated angle = Θ / 12 / 2 rad or 15 degrees. We find r = 1.01152. The enclosing circle has a radius that is 1% or one centimeter longer than the meter.

A slice of Θ / 12 of the polygon: The inner circle has r = 1 and h = Sin[Θ / 24] = 0.2588, the outer circle has r = 1.01152 and h = 0.5236 / 2 = 0.2618.

Ai Weiwei without his nudes

This weblog has a serious topic – the boycott of Holland till the censorship of economic science is lifted – but it must also contain an element of humour, or, at times, even some joyful variety with song and dance and good drinking, to prevent an atmosphere of gloom and doom. Little is sadder than censorship, but, oh yeah, sadder is the voice of protest that is hardly heard and not reported on in the Financial Times. Nobody wants to read page after page of protest, this continuous wail, even if it shows good reasoning and sound advice.

Entertain or perish. Thus this weblog must show a lightness of heart, an openness of mind to the wealth outside of censorship and protest. John Maynard Keynes had his Essays in Persuasion that still make great reading. John Kenneth Galbraith accepted that others bested him in mathematics and developed his literary style to penetrate into deeper questions. The economy depends upon money but also upon talk. Klamer & McCloskey calculated that 40% of GDP was taken by rhetorics. An increase in productivity in this part of the economy requires the development of better narratives. Professor Yiannis Gabriel at the university of Bath studies the narratives in organisations, and uses his skills to comment on developments in Greece. With such examples, we should not only look at the Greek Tragedy in its Land of Origin but employ our openness of mind to also include the other side of the world.

When we speak about humour, joyful variety, that dance of the mind, that enchantment of suddenly new insights, then we naturally think about Ai Weiwei. Earlier this weblog focussed on his nudes but apparently he will take a seat in the jury for the Tiger Awards at the International Film Festival Rotterdam, January 23 – February 3, though without his nudes, and without actually coming to Rotterdam since the Chinese authorities think that it is better that he stays home and uses the internet. We are thus faced with a double absence of artistic inspiration. It is not impossible that Ai thinks that there aren’t enough Dutch ladies to give him a proper nude welcome in Rotterdam and that he merely inserts the government for a lame excuse. Alternatively, Dutch nudes will flock to Rotterdam and dance about to emphasise his absence, or rather jump around to keep warm in the present cold winter.

There is a peculiar difference in censorship between the (relatively) free democracy of Holland and the military dictatorship in China.

In Holland the narrative of democratic freedom turns against the victim of censorship. In a democracy there cannot exist censorship, is the axiom. The world has seen the paedophilia in the church, Jimmy Savile at the BBC, Lance Armstrong in bicycling, … and numerous other cases where freedom was quite infringed upon, and, also, for an amazingly long time. The curious (?) thing about the problem at the Dutch Central Planning Bureau is that it hasn’t anything to do with financial corruption, graft, sex, drugs or rock ‘n’ roll, but quite interestingly merely with economic theory and integrity of economic science. Still, the axiom is – John Kenneth Galbraith coined the term conventional wisdom – that there cannot be censorship of science at the Dutch Central Planning Bureau. Another axiom is that, even if there would be such censorship, then it would not be relevant for the Dutch export surplusses and current economic crisis and what other economists babble about. Subsequently it would not be useful to study the issues of the tax void, the dynamic marginal tax rate or the Economic Supreme Court. Hurray, no need to boycott Holland. Go, you blind people, I would say, go, and wash your eyes.

In China the narrative of dictatorship supports the economic development of the nation, up till a point where less than 40% of GDP is taken by rhetorics and where other narratives have to take over. For the Chinese dictatorship, I would not try to phantom their dilemma’s and the position of Ai Weiwei. The only suggestion that I can think of is a plan with a longer horizon. The current economic development in China came about by fixing the state enterprises at their levels of operation and allowing the new growth to come from new freeer upstarts. This strategy by Deng Xiaoping has taken some decades but produced wonders. In this line, the current leadership might draft a plan for a transition period of two decades with step by step changes in the narrative to eventually national democratic elections (see my book Voting Theory for Democracy). World developments are so fast that three decades would be too long. Sticking to the plan would enhance credibility. A prime focus would be on rule of law and basic economic security for everyone. In seven years there might be a free press on local issues, in twelve years on national issues. Well, who am I to suggest this ? The Chinese are quite capable of running their country, and we will see whether Ai Weiwei inspires them and can be more free to travel when he turns 75. An older artist, with older nudes, such is the tragedy of life, but perhaps still agile enough to drink and dance, in a possibly somewhat warmer Dutch winter.

How CofFEE becomes latte

When you order latte in Holland, the Dutch term is ‘koffie verkeerd’, which translates as ‘wrong coffee’. Proper coffee clearly doesn’t have milk (or perhaps a few drops but certainly not as much). Tastes differ but it is a tell-tale that latte is labelled as wrong coffee.

In economics there is a research group calling themselves CofFEE, or the Center of Full Employment and Equity, at the University of Newcastle, Australia. They collaboratie with the Center for Full Employment and Price Stability (CFEPS) at the University of Missouri, Kansas City, USA. Perhaps the suggestion is that the University of Chicago is the Center of Unemployment and/or Inequity and/or Price Instability.

Full employment is a key Human Right, and full employment is cheaper than giving benefits to the unemployed. Thus full employment is a no-brainer. That nations do not have full employment is a sign of failures in the policy making process. CofFEE presents a rather unattractive form of full employment, labelled the ‘job guarantee’. A better form that mainstream economists will tend to like uses my analysis on the tax void and the dynamic marginal tax rate. Apparently Economic Supreme Courts are required for democratic nations to prevent the failures in policy making.

My suggestion is that things are not okay in Holland. Does this apply in this case too ? Unfortunately it does. No exception on no-brainers. There exists CofFEE-Europe, located at Maastricht University, where there is a problem. Because of this problem, CofFEE turns into latte (invent your own abbreviation). Full employment, i.e. a basic approach on employment, is turned into a weak derivative with perhaps a cult status for a minority of the fancy but unconvincing for the mainstream.

Professor Bill Mitchell of CofFEE presented his unattractive form of full employment at the EU Commission, see this video. The chair is by Koos Richelle, Director General for the European Commission’s DG Employment, Social Affairs and Inclusion, who happens to be a Dutchman. See this video with Richelle’s approach to the issues, which shows that he would be interested in a sound argument for full employment. Thus, Mitchell’s presentation at the EU was a missed opportunity of economic science to present that sound argument.

Where did economic science go wrong ? Well, there is censorship of science at the Dutch Central Planning Bureau (CPB) since 1990, and there is the refusal of Dutch professors of economics to protest against this. One of these professors is Joan Muysken in Maastricht at CofFEE-Europe. He didn’t study my analysis and may not have told Bill Mitchell about it. In that manner the flow of information gets stuck. In that manner a no-brainer turns into not using our brains.

In 1990, at the CPB, I wrote this paper on unemployment with the advice of a parliamentary enquiry. I actually was invited by professor Muysken to present it in Maastricht. Given the lack of response since then I infer that he may have read the paper but did not study my analysis. The paper was blocked by the directorate of the CPB, with no internal discussion and external publication, and I was dismissed with lies and an abuse of power.

In 1998 I collaborated with journalists Hans Hulst and Auke Hulst in a Dutch booklet on unemployment and poverty, with the title ‘Werkloosheid en armoede, de oplossing die werkt’, Thela Thesis, Amsterdam. The booklet was targetted at a general audience and referred to my scientific papers for the evidence. There is also a state newspaper in Holland in which the government must print its laws to have them become effective, the ‘Staatscourant’. It so happened that professor Muysken wrote a review of the booklet for that Staatscourant. In summary, he enjoys that the issue of full employment is put on the table again, but dismisses the analysis in the booklet as insufficiently scientific. However, he did not study the underlying analysis and evidence. Now this is quite silly and rather sick. The booklet is for a general audience, thus it should not be treated as a scientific exposition. The booklet was intended to raise the attention level of the general public and to draw attention of my fellow economists to the underlying studies. By declaring that the analysis was inadequate professor Muysken killed those prospects. Curiously, Muysken did not respond to my reply on this and my invitation to study the underlying work. Curiously, he hasn’t done so in 1998-2012, even though there is DRGTPE since 2000 that integrates the analysis, and even though there is an economic crisis since August 2007 that confirms the analysis. I haven’t read the Mitchell & Muysken (2008) book since its summary suggests an inferior analysis to DRGTPE, and my bet is that they do not refer to DRGTPE.

What is it, that causes Dutch professors of economics to be so unscientific ? It is not that they are mere human beings, that is too easy. Yet it is something that a good boycott of the country may help to resolve. Perhaps you want to read this weblog entry again, with a good cup of coffee to get your brain working.