Trigonometry rerigged 2.0
Trig Rerigged 2.0 (draft) proposes a new didactic approach to trigonometry. The proposal has the form of a booklet since it reprints some pages from Elegance with Substance (2009, 2015) and A child wants nice and no mean numbers (2015). The format might change in the future, like the earlier discussion of Trig Rerigged 1.0 of 2008 (now legacy) was absorbed in Conquest of the Plane (2011).
The reader might start with page 15 with the main idea, and page 16 with the main graphs. When these make sense, then restart at the beginning. Trig Rerigged 2.0 is targeted at researchers in mathematics education, teachers of mathematics and trainers of teachers. Well, science journalists might step in too. When you are none of these, then you are advised to be satisfied with the following.
Angular circle with circumference 1. Hook disk with area 1
A circle is defined as the collection of points at a given distance from a center. This distance is called radius. The circle is a concept of circumference. There is proportionality with the radius. With radius r we have circumference r Θ.
A disk is defined as the collection of points at a given distance or less from a center. The disk is a concept of area. Area depends upon the square of the radius. The general disk area is π r 2. Areas of concentric disks however are proportional again.
The unit circle has radius 1 and circumference Θ (“archi”) and disk area π (“pi”). Also Θ = 2π.
The angular circle has circumference 1. Angles can be measured as arcs on the angular circle, as percentages of 1. The angular circle has radius ΘH. It is common to use the algebraic symbols instead of their numerical values Θ ≈ 6.28… and H = -1 (“eta”).
The hook disk has area 1. Angles can be measured as sectors on the hook disk, as a percentage of 1. The hook circle has radius √πH.
Main conclusions
- It is immaterial whether angles are measured as arcs on the angular circle or as sectors on the hook disk. In both cases we have perunages or percentages of 1. The unit of measurement is actually the plane itself. Another formulation is the number of turns around a circle.
- Both Θ and π are useful symbols to denote these relationships. They support a rich didactic environment, that allows students to grasp the notions that are closer to their understanding, and develop from there.
Graph of angular circle and hook disk
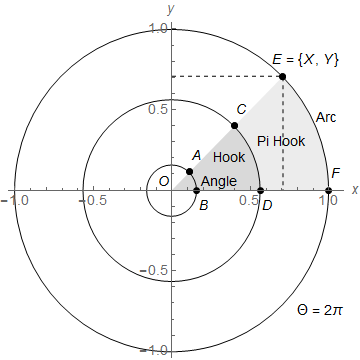
The following graph from page 16 gives the notions in a nutshell.
The angle α is the arc AB along the angular circle, or the sector OCD on the hook disk. When the sector is extended from the hook disk onto the unit circle, then this sector might be called a “Pi hook”, for its value is α π.
The arc EF is the angle in radians, with the value α Θ.
The point {X, Y} = {x, y} rH has the property that X2 + Y2 = 1. It is useful to use the separate symbols X and Y for this point, since it determines the length of arc from {1, 0}. The point on the unit radius (ur) circle can also be described as a function of the angle α, as {X, Y} = {Xur[α], Yur[α]} = {Cos[α Θ], Sin[α Θ]}.
 Potential implementation
Potential implementation
Since these are suggestions for improved didactics, there must be empirical testing to determine whether these are improvements indeed. It are the students who must show that it works.
Earlier I discussed the US Common Core. This new development on the didactics of trigonometry can be included. See Trig Rerigged 2.0 for more on the relationship to the US Common Core.
I am not qualified for primary education, but the above would seem to be helpful. For example, young pupils could colour sectors of the hook disk, and determine that hooks are additive. At a next stage, they may see the frailer circumference, and see that e.g. 25% of hook matches with 25% of angle. The pupils would be able to determine the radii of the hook disk and the angular circle, so that they grasp proportionality, and that area goes by the square of the radius, and the relationships to Θ and π.
There is an intermediate stage at which {X, Y} = {Xur[α], Yur[α]} = {Cos[α Θ], Sin[α Θ]} will be discussed, and their inverses. Parts might already be done in elementary school, but it would surely be done (repeated) in the early phase of secondary education. PM. The animation at wikipedia for the sine is fairly good, but one would want to be able to manipulate the position, and the choice of yellow for the vertical position is too light.
At the end of highschool, students should be able to deal with radians and sine and cosine. Those functions remain key because of the derivatives. However, the working horses will likely be Xur and Yur, for in trigonometry it is natural to work with turns.
Acknowledgement and word of protest
Above idea basically builds upon Trig Rerigged 1.0 from 2008. The issue here is didactics of trigonometry.
Michael Hartl published a tau manifesto in 2010, and MSC published a reply pi manifesto. The issue here is rather curious. Hartl explains his approach: “π is a confusing and unnatural choice for the circle constant.” This doesn’t concern didactics but concerns some notion of naturalness in some mathematical universe, as if criteria in mathematics itself would force a choice between either Θ or π. I don’t think that this is a relevant way to formulate the issue or discuss it. There is no need for an “archi manifesto” since the relevant issue has been stated in terms of didactics of mathematics in above books. Also, tau is an awkward choice of symbol, for it looks too much like the symbol r for the radius, especially in the handwriting of students.
Still, I read these manifestos and benefited from aspects of them, notably since this gave me the idea to define the hook disk as the disk with area 1, so that we can better see the underlying unity of the notion of angle or hook. Thus I acknowledge the contributions, but also must protest that it doesn’t help when these manifestos divert attention away from the proper question on didactics.
Earlier weblog texts on this issue have been here and here and this animation. On the use of H, see here.
